Donna left a great comment on the last blog entry.
“If I want to sew a HST to a side of a square, and I know the size of the side of the square (say, 2″), and I know that the diagonal of the HST has to be 2″ (duh!), what is the finished size of the HST going to be? Is there a formula for that?”
This is a great question. Yes, there is a formula, Donna.
We either multiply or divide, depending on which measurement we know.
The “magic number” is 1.414.
Yes, really. 1.414. I apologize.
In Donna’s example, the triangle would be 1.414 inches (finished), and it is available in an Inklingo shape collection.
Let me explain.
1.414 was discovered thousands of years ago by Pythagoras (left), and re-discovered by Monkey (right) when I was writing The Inklingo Handbook. LOL Luckily, someone had invented a calculator in the meantime.
Inklingo quilters only need a passing familiarity with Pythagoras (born about 570 BC), his theorems, hypotenuses, and square roots.
Just remember 1.414. That’s enough.
Monkey says:
- If you know the number should be bigger than the one you know, multiply.
- If you know the number should be smaller than the one you know, divide.
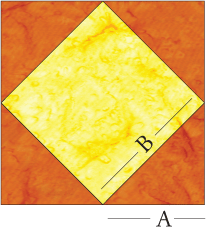
If you know that B is 3 inches (finished size),
to get A, we divide by 1.414. A = 2.12
If you know that A is 3 inches (finished size),
to get B, we multiply by 1.414. B = 4.24
In Donna’s example, if we know B is 2 inches, we divide by 1.414, and A is 1.414. (That is spooky, until you realize that the square root of 2 is 1.414. Getting into deep water here. Quilters don’t need to know about square roots.)
When your calculator gives you the finished size, you can check to see if it is available by going to the Inklingo Index of Shapes (under the Support tab on inklingo.com).
2.12 inch HST? YES! Available! So are 1.41 inch HST. Isn’t that cool? Also 4.24 and 2.83 and others. Designs like Storm At Sea are chock full of weird measurements like this, but you don’t have to fear them anymore!
If anyone had told me 40 years ago how useful geometry would be to me now, I would not have believed it. Since Inklingo, Pythagoras and I are BFF.
NO MATH !
Hooray! Inklingo does all the work for you. You just print precise shapes on fabric with your ordinary Inkjet printer. No measuring, no fuss. Perfect shapes. Even Storm At Sea becomes easy. (Get the design book—$10 or free!)
ANOTHER LOOK
In many cases, quilters start with the finished size of the whole block, and work backwards to get the finished size of the triangles and the square.
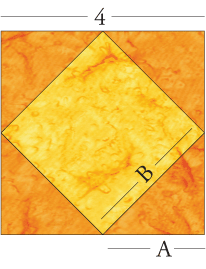
For example, if you know you want the block to be 4 inches (finished),
A = 2
A x 1.414 = B = 2.83
When we look in the Inklingo Index of Shapes, we see that the squares and HST are available in one of the shape collections. Life is good.
INKLINGO INDEX OF SHAPES
There are several odd-looking sizes in the Index of Shapes. Now you know why.
More resources:
- Snowball block Video
- Triangle Tips PDF
- The Inklingo Handbook, pages 114 and 115 discuss the magic number 1.414
Whew! Thank you, Donna, for a great question!
Linda & Monkey
PS Don’t forget to leave a comment HERE to have a chance to win a $25 Gift Certificate on Mother’s Day!
New to Inklingo? Order and download free shapes and start sewing in the next few minutes. Quick Start (Always FREE.) There are triangles, diamonds, and squares in the free collection—great for dozens of different blocks.








Hi Maria, I think the measurements are simpler than you are imagining.
For all of history, quilt designers have rounded numbers to make them easy to measure, or have used templates, with the result that the actual measurements were a secret. No one would dare ask a quilter to cut something “a little bit smaller than 1-7/8 inch” (i.e. 1.86) or “about 1-1/3 inch” (1.32), but that is what you need for a LeMoyne Star block that finishes 4.5 inches (Dear Jane size).
It’s a wonder we got good results at all with all of the rounding and fudging that went on. With Inklingo, we can be absolutely precise, so everything matches perfectly without the bother of weird measurements or templates and tracing. It also makes much complex blocks possible for quilters with less experience.
Dear Linda & Monkey,
Thank you for reminding me of this. I have learned it several times, and all I remember each time is that ‘there is something important’ about 1.414, which in practice is not a very useful memory. Seeing the pictures definitely helps!
Hugs, Anneke in Rotterdam
Linda – You and Monkey are quite the renaissance thinkers! I’m not a math person at all, and I really have to be careful about figuring out piecing calculations. When I downloaded the free Triangle shape collection, the one thing I couldn’t figure out was the relevance of the shapes’ sizes. They seemed really unusual. I didn’t see the traditional 2,”, 2-1/2″, or 3″. The measurements were all something like 1.61″ (I’m doing this from memory and probably getting it wrong, but I found it a bit confusing.) Can you clarify this for me and all the other non-math thinkers out there? Thanks Linda!
thank you Monkey
for this GREAT lecture – that was exactly what I wanted to know for some time. Seems I wasn’t paying enough attention to my math teacher many moons ago
greetings to Linda from Germany
Brigitte
Whew! Great post. I’ve been working with Pythagoras’ equation, but this is way simpler ! Thank you.
Wow! You and Monkey are geniuses! And I think Monkey looks a lot like Pythagoras, don’t you? Especially around the eyes…
I know most quilters will be thinking of finished sizes and will work backwards to figure out the center square, but I have a lot of pre-cut squares already, and am always puzzled about how to frame my UFO blocks. So starting from the inner square and working outwards really works for me!
And how great is it that you already have collections with “my” measurements? (HST/Square speaking of course!!!)
I’ll be thinking 1414 with a point after the first 1, multiplied up or down depending on which is bigger. But just in case, I’m going to print this out and bookmark it!
Thank you bunches of perfect HSTs! 🙂 🙂 🙂